SPIN ESR 3.1: Optimal Design of Experiments and Surveys for Scientific Interrogation
Name: Dominik Strutz 
Institution: University of Edinburgh, U.K.
Email: domink.strutz@ed.ac.uk
Introduction
My passion for the planet beneath our feet is what brought me to geophysics. The combination of classical mechanics, fascinating geological processes and high-performance computing applied to usually inaccessible structures is what keeps me fascinated to this day. Exactly this inaccessibility makes inverse problems - converting data to models of the subsurface - so vital to geophysics. Any optimization in this process will lead to a better understanding of the world around us.
Most of the time, data is taken as given in inverse problems. In my project, I take a step back and investigate how much the design of an experiment can influence the expected results. The next step is choosing an experimental setup that is most likely optimal in giving the most information about the subsurface given a typical dataset.
While based on a straightforward theoretical framework, solving this problem in practice is computationally very expensive, if not infeasible, even for small-scale experiments. My work over the following years will mainly focus on finding approximations that allow designing extensive surveys of one or several sensor types optimally.
After finding these methods, I will focus my research on how to design experiments to answer specific questions such as: “What’s the size of a certain subsurface body?” or “Is the source of micro-seismicity moving upwards?”
All of the methods I plan on using extensively use concepts from statistics and machine learning, and I am very excited to learn more about those to complement my geophysics background.
Finally, I want to thank the SPIN project for giving me the unique opportunity to work on this project as part of a Marie Skłodowska-Curie Actions EU grant.
For more information about me you can also visit my academic webpage.
Publication
Research progress
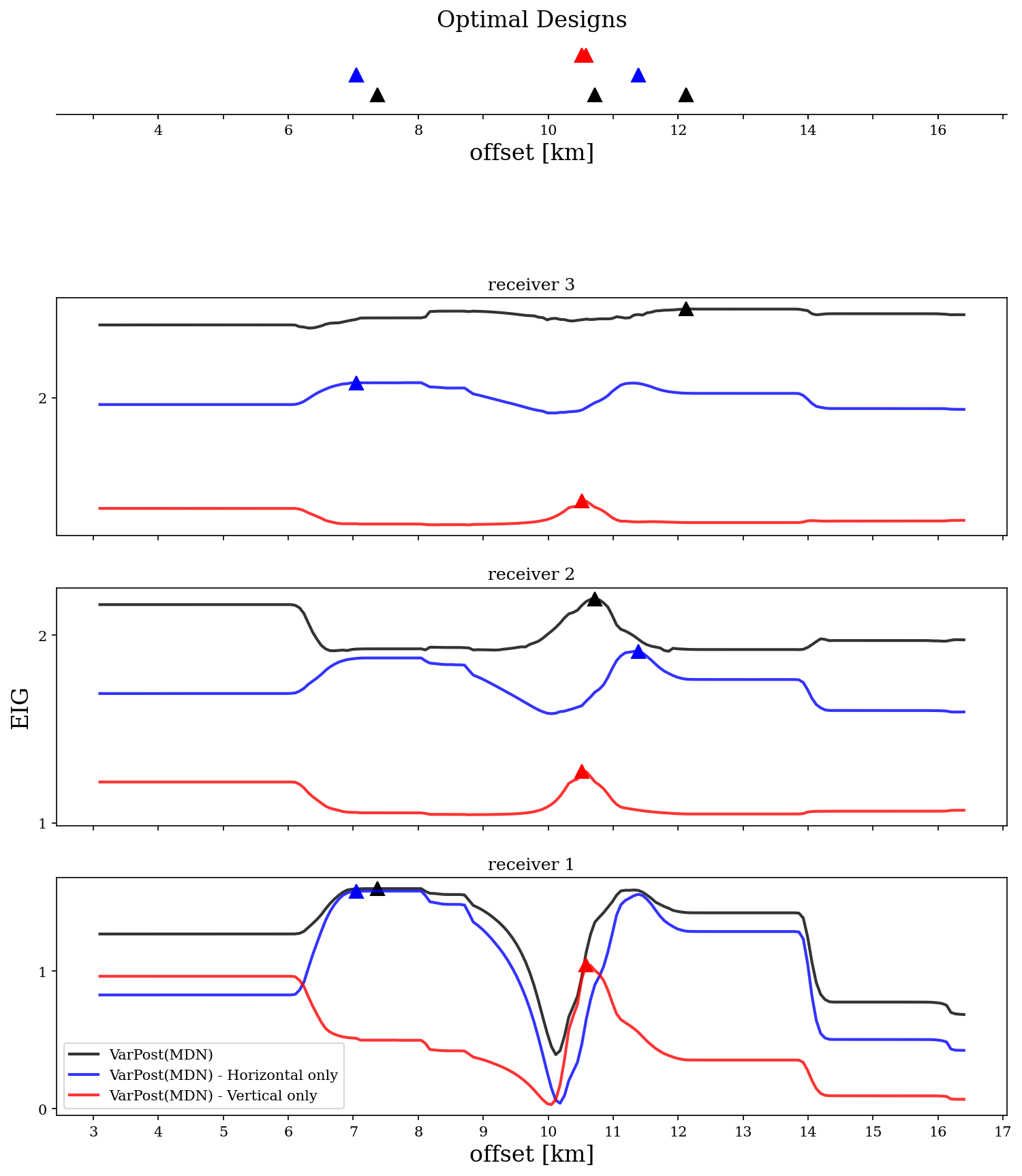EIG optimisation results for a sequential constructive design optimisation for three receivers in a seismic source interrogation problem. The intermediate steps for receivers one and two are also shown, with the optimal receiver depicted by a triangle in the colour corresponding to the respective interrogation aim. This shows that optimal design can be used to answer the questions: ‘What is the best design to constrain the depth/epicenter of a seismic source?’
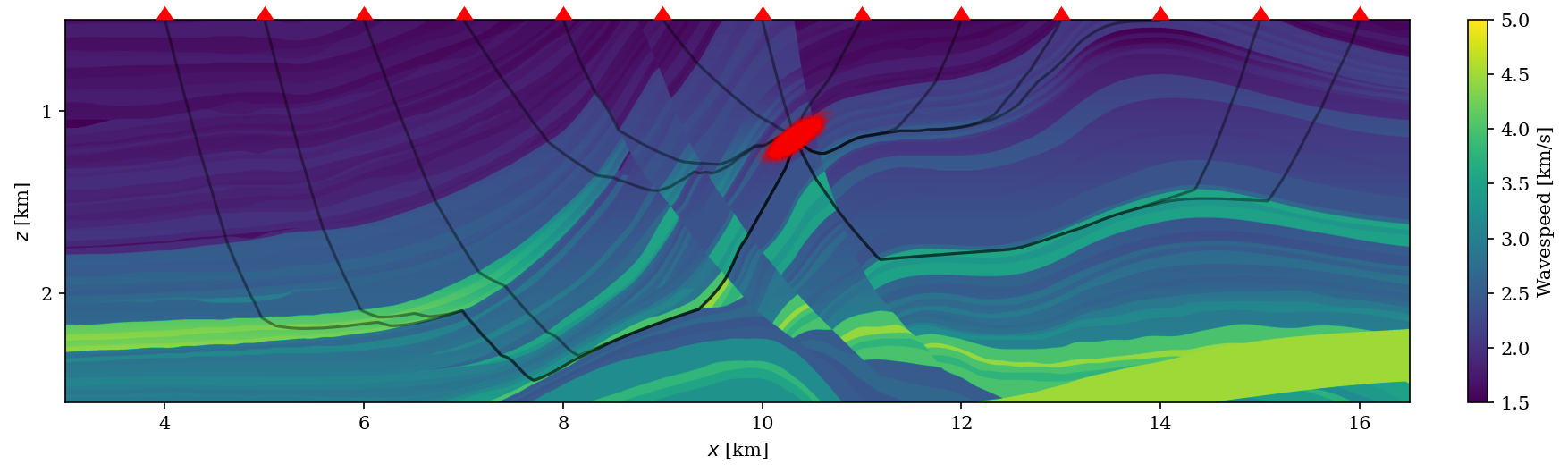Seismic source location problem setup with prior samples (red dots) and seismic rays to an exemplary set of receivers (thin black lines) originating from one of the prior samples.